[03] Relations and Functions

Cartersian product

 

Binary relation

a set of oredered pair로 나타낸다. set이기 때문에 set의 연산이 모두 가능하다.

 

 

Binary relation은 두개의 pair의 관계를 나타낸 것이고 3개면 ternary, 4개면 quaternary라 한다. 표기는 다음처럼 한다.

 

Ternary relation

4개일 때, n-ary일 때 모두 같다.

 

Properties of Binary relations

Reflexive relation

(a,a)가 R에 있는 경우

 

Symmetric relation

(a,b)가 R에 있으면 (b,a)도 있는 경우

 

Empty set U={}인 경우에도 성립한다. 대신 reflexive는 만족하지 않는다.

S={(a,a)}면 symmetric이다.

 

Antisymmetric relation

a와 b가 다른 경우에, (a,b)가 R에 있으면, (b,a)는 없는 경우

 

순서관계가 중요한 경우에 주로 사용된다.

 

S={(a,a),(b,b)}는 antisymmetric

S={(a,b),(b,a),(c,c)}는 antisymmetric이 아니다.

 

Transitive relation

(a,b)와 (b,c)가 있을 때, (a,c)도 R에 있는 경우

 

S={(a,b)}도 transitive다.

S={(a,b), (b,c)}면 transitive가 아니다.

 

Transitive closure

Transitive를 만족하게 계속해서 확장해볼 수 있다. 

S={(a,b),(b,c)} $\rightarrow$ $S_1$={(a,b), (b,c), (a,c)}

 

확장하다보면 더 이상 변하지 않게 된다. 그 때를 transitive closure라고 한다.

 

Equivalence relation

• reflexive
• symmetric
• transitive

위 3 조건을 만족하는 경우이다.

 

위의 테이블을 보면 알겠지만, partition하기 편한 구조로 나오게 된다. 그리고 relation이 줄어들면, partitioning은 더 작게 된다.

 

Partial Ordering relation and Lattices

Partial ordering relation

• reflexive
• antisymmetric
• transitive

위 3 조건을 만족하는 경우이다.

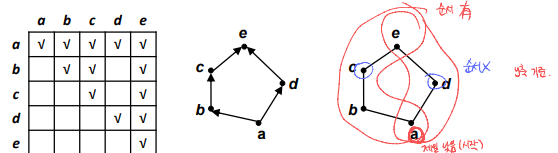
위 테이블(왼쪽)처럼 나타내기도 하며, graphical(가운데), Hasse diagram(오른쪽)으로 나타내기도 한다.

 

Partially Ordered Set

POSET이라고도 한다. Partial ordering relation을 만족하는 set을 의미하며 $(A,R)$로 표현한다.

 

Chain

POSET의 subset을 말하며 chain의 length는 element의 수를 의미한다.

 

Antichain

두 element가 subset으로 존재하지 않는 경우, antichain이라고 한다.

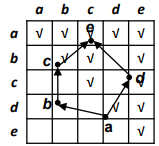
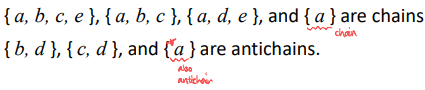
{a}와 같이 단일 친구는 chain이면서 antichain이다.

 

Totally ordered set

TOSET이라고 하며, 모든 element 사이에 관계가 있는 경우를 말한다. Antichain이 없는 경우이다.

 

Notions of POSET

#POSET에 대해서 Maximal element와 Minimal element를 정의할 수 있다.

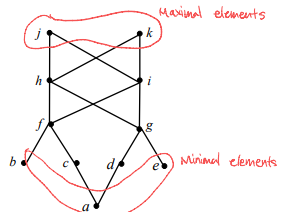
이와 별개로 greatest element와 leastest element는 1개이거나 없을 수 있다.

 

#Upper bound와 least upper bound를 정의할 수 있다.

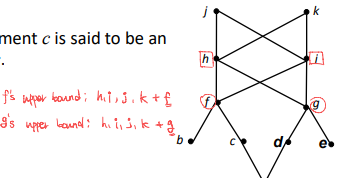
upper bound는 자기 자신을 포함한 상위 element이고, least upper bound는 그 중 제일 가까운 element이다. f와 g의 least upper bound는 h와 i이다.

 

#Lower bound와 greates lower bound도 정의할 수 있다.

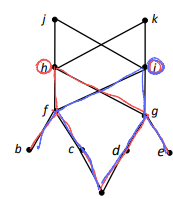
lower bound는 자기 자신을 포함한 하위 element이고, greatest lower bound는 그 중 제일 가까운 element이다. h와 i의 greatest lower bound는 f와 g이다.

 

Lattice

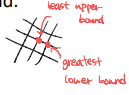
POSET에서 아무거나 2개 element를 선택해도 least upper bound와 greatest lower bound가 1개씩 unique하게 선정되는 경우이다.

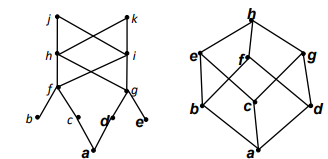
왼쪽은 lattice가 아니지만, 오른쪽은 lattice이다.

 

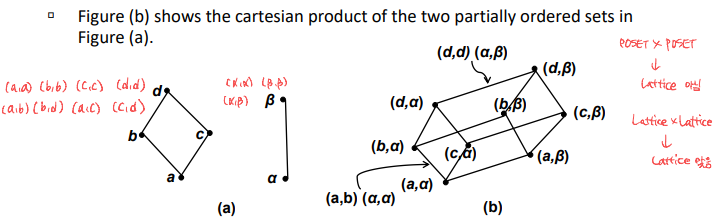
POSET×POSET은 lattice일 수 있고, Lattice×Lattice는 Lattice이다.

 

Chain and Antichain

Binary relation$(P,R)$에 대해서, longest chain의 길이가 n이라면, $P$에 있는 element는 antichain n개로 partitioned될 수 있다. Induction으로 증명 가능하다.

 

Antichain의 partition은 여러 방법으로 가능하다.

 

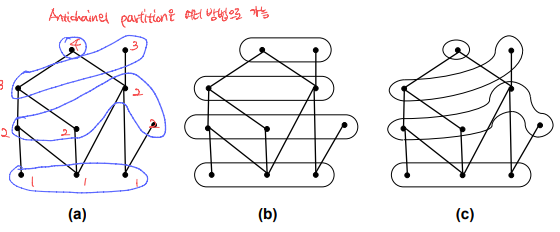
Corollary도 있는데, $mn+1$개의 element로 구성된 POSET은 $m+1$의 element로 구성된 antichain을 가지거나 $n+1$의 길이의 chain을 가진다.

 

이는 contradiction으로 antichain의 원소가 m개, chain의 길이가 n보다 작은 경우를 가정해서 증명하면 된다.

 

Pigeonhole principle

(a) onto (b) one-to-one (c) one-to-one onto

 

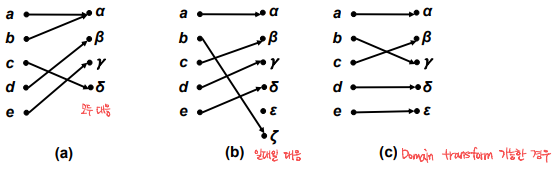
비둘기집의 원리는 $|D| > |R|$의 유한한 set에 대해서, $f(d_1) =f(d_2)$로 대응시킬 때 겹치는 경우가 있음을 의미한다.

 

#문제

 

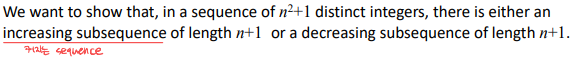
$x_i$와 $y_i$는 각각 sequence에서 시작하는 incresasing subsequence, decreasing subsequence의 길이라고 가정해보자. Contradiction을 이용해 증명한다. 둘다 n보다 작다고 가정해본다.