디지털 통신 시스템의 Error-correcting code는 다음과 같다.

$R<C$면 error-free 통신이 가능하지만, 다양한 이유로 에러가 발생할 수 있고, 이를 수정할 수 있는 코드가 필요하다. 방법은 다양하게 구현되어 있다.
- Syndrome checking
- Cyclic Redundancy Check (CRC)
- Applications: Automatic Repeat reQuest (ARQ)
가장 나이브한 방법은 Message size를 알고 그에 따른 codeword를 알고 있을 때, received된 codeword와 table에 있는 codeword의 유사도를 비교하는 방법이다.
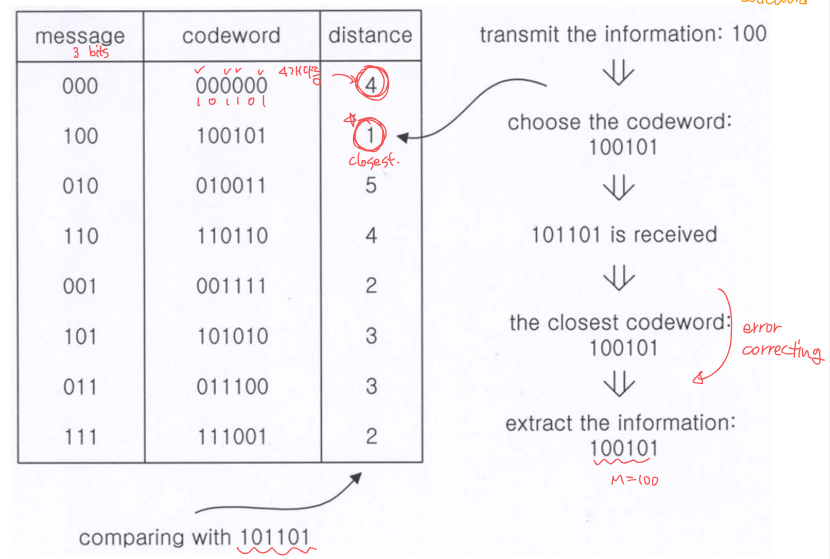
위 방법은 $2^3$개의 table row를 요구하기 때문에, k이 작은 경우에만 사용할 수 있다.
유사도는 어떻게 비교할까?
- Hamming distance : 다른 bit의 수를 세기
- Hamming weight : nonzero bit의 수를 세기
- Binary case : $d(u,v)=w(u\, xor\, v)$
1. Maximum-Likelihood Decoding (MLD)
$$ p(v|r) = {p(r|v)p(v) \over p(r)} $$
Optimal decoding rule은 $p(v|r) = max_s p(s|r) $하는 거다. (MAP decoder) 그리고 이거는 ML decoder로 불리기도 한다.
DMC (discrete memoryless channel)을 가정하게 되면, 식은 더 쉬워진다.
$$ log p(r|v) = max_s log p(r|s) $$
BSC channel의 경우 다음처럼 바꿀 수 있다.

$log p(r|v) = d(r,v) = min_s d(r,s) $
$p(r|v)$를 maximize하는 것은, $d(r,s)$를 minimize하는 것과 같기 때문이다. 그래서 BSC의 optimal decoding rule은 $d(r,s)$를 minimize하는 것이다.
Coding theory에는 3가지 문제가 있다.
- Good code 찾기 (random이 보통 좋음)
- Decoding algorithm 찾기 (low complexity)
- Decoding algorithm 구현 할 방법 찾기
Note: [n,k] code
- Transmission rate n/k 증가
- Channel bandwidth 필요 n/k 증가
- Message transmission rate k/n 감소 = FEC (Forward Error Correction) 비용임
2. Classification of FEC
- Block code
- Tree code
- Linear code
- Nonlinear code (실제 시나리오에서는 안씀)
- Systematic code
- Non-systematic code
Channel capacity of AWGN simple channel is $C=B log_2 (1 + {S \over N}) $.
보통 -1.6dB 이상의 SNR을 요구했음.

3. Linear Block Codes
Generator와 Parity-check matrices의 조합임

[n,k] linear block code over $F_q = GF(q)$, ${log_q q^k \over n} = {k \over n}$.

그래서 $c=mG$

Geneartor는 다음처럼 만들 수도 있음 (특별한 경우, [7,4] Hamming code)


그래서 $Hc = 0$, $GH^t = 0$
$r = c+e$고 $Hr = H(c+e) = Hc + He = He$여서 error 위치를 검출할 수 있는 것을 syndrome이라고 한다.

Hamming code는 error 1개만 수정가능하다.
Hamming distance와 weight는 다음의 관계를 가지고 있다.
$$ d_H(x,y) = w_H(x-y)$$

$t_c$ error correcting과 $t_d$ error detecting 코드는 ($t_d \geq t_c$) $t_c$ 이하의 에러를 수정할 수 있다.
$$ t_c + t_d +1 \leq d_{min} $$
반대로 $d_{min}$이 주어지면, $$ 2t_c + 1 \leq d_{min}$$
$t_c = {d_{min} - 1 \over 2}$는 error correction capability임


4. Dual codes


'Study > Coding and Information Theory' 카테고리의 다른 글
| [09] Cyclic Codes (1) | 2024.06.11 |
|---|---|
| [07] Channel Capacity (1) | 2024.06.09 |
| [06] Data Compression (1) | 2024.06.08 |
| SUMMARY (1) | 2024.04.10 |
| [05] Entropy Rates (1) | 2024.04.10 |
