[03-1] Entropy, Relative Entropy & Mutual Information
Uncertainty
Random variable X에 대해서 X가 discrete하거나 continuous한 경우, 다음처럼 확률을 표현할 수 있다.
- Discrete (pmf) : $P(x) = Pr\{X=x\}$ where $\sum P(x)=1$
- Continuous (pdf) : $\int f(x) dx = 1$
- cdf = $F(x) = Pr(X \leq x)$
- $f(x) = F'(x)$
확률을 보고 uncertainty를 결정할 수 있다.
- Low Prob. = High Uncertainty
- High Prob. = Low Uncertainty
예를 들어서, coin toss를 하는데, head가 나올 P가 1이면, uncertainty는 0이 된다. 확실하니까
Entropy
Uncertainty를 측정하는 단위이다.

Entropy는 RV를 표현하기 위한 최소 bits 수를 의미하기도 한다. Coin toss를 예를 들면, 다음처럼 entropy를 측정할 수 있다.

Entropy는 다음의 특징을 가진다.

다음처럼 사용할 수 있다.

Joint Entropy
Random variable 2개에 대한 joint distribution의 entropy를 joint entropy라 한다.

다음과 같은 joint distribution이 있으면 joint entropy를 구할 수 있다.

Conditional Entropy
Conditional probability는 Bayes' rule에 의해 다음처럼 결정되었다.

$p(x=1|y=1) = \frac {p(x=1, y=1)} {p(y=1)}$처럼 사용했다.
Conditional entropy는 다음처럼 구할 수 있다.

예제를 보면서 이해해본다. !!!! 이거 틀림 !!!! $H(Y|X=1)$을 구하기 위해서는 써있는것처럼 하는게 아니라 $p(Y|X=1)$을 구해서 해야함

Chain Rule of Entropy
$H(x,y)$를 정리해보면 다음과 같은 관계식을 얻을 수 있다.

그래서 정리하면 다음과 같다.

쉽게 설명하자면, X와 Y의 entropy는 X의 entropy와 X가 관측되면서 줄어든 Y의 entropy의 합이라 생각하면 된다.
Relative Entropy
확률 distribution 2개의 거리를 측정하는 방법이다. 실제 분포가 $p$일 때, $q$라고 가정하는 것의 비효율성 척도라 생각하면 된다. 한마디로 크면 구리다.

Kullback-Leibler distance라고도 알려졌다. 예제는 다음과 같다.

일반적으로 $D(p||q) != D(q||p)$이다.
KL divergence & Cross Entropy in ML
(참고)Entropy는 $H(x) = \sum p(x) log p(x)$였다. CE loss는 일반적으로 다음처럼 사용한다.
$$ CE_{loss} = - \sum t_i log P_i $$
실제 예시를 보면 다음처럼 확률분포간의 차이를 학습할 수 있음을 알 수 있다.
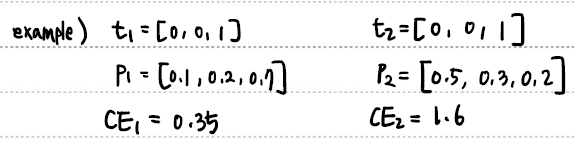
잘 보니 KL divergence와 유사하다. 실제로 KL divergence를 구해보면 유사함을 알 수 있다.

$\theta$에 영향을 받지 않는 부분을 날려버리면, $CE=-\sum t_i log P_i$임을 알 수 있다.
Mutual Information
Entropy가 정보의 uncertainty를 나타내는 것이었다면, Mutual information은 RV X와 Y가 공유하고 있는 정보량을 의미한다. 수식으로 다음처럼 사용한다.

KL divergence로 표현하면 $D(p(x,y) || p(x)p(y))$이다.
Entropy와의 관계
$I(X:Y)$를 정의에 따라 정리해보면, entropy와의 관계를 얻을 수 있다.

이를 통해서, X와 Y의 공유하고 있는 정보량은 사실 Y 정보가 주어졌을 때 X 정보의 uncertainty 감소량이라는 것을 알 수 있다.
Entropy and Mutual Information

Chain Rule for Entropy

하나가 주어졌을 때, 다른 친구의 entropy를 더해가는 식으로 RV의 entropy를 구할 수 있다.
Conditional Mutual Information

Entropy처럼 Z가 주어졌을 때, Y를 알았을 때 감소하는 X의 uncertainty라고 생각하면 된다.
다음의 chain rule을 가진다.

벤다이어그림으로 나타내면 다음의 관계를 가진다.

Conditional Relative Entropy
pmf $p(x)$에 대해 평균을 낸 conditional pmf $p(y|x)$와 $q(y|x)$ 사이의 Relative entropy의 평균이라고 생각하면 된다.

다음의 chain rule을 가진다.

'Study > Coding and Information Theory' 카테고리의 다른 글
| [05] Entropy Rates (1) | 2024.04.10 |
|---|---|
| [04] AEP, Asymptotic Equipartition Property (0) | 2024.04.10 |
| [03-2] Jensen's Inequality (0) | 2024.04.09 |
| [02] Brief review of Probability (1) | 2024.04.09 |
| [01] Introduction to Information Theory (1) | 2024.04.09 |
