String matching
Text $T$(len: n)에서 pattern $P$(len: m)를 찾는 문제입니다.
Naive algorithm
쉽게 생각해보면, 모든 text 위치에서 pattern을 검사하면 string matching을 수행할 수 있습니다. 이 때의 시간 복잡도는 $O(nm)$입니다.
Rabin-Karp algorithm
Hash를 이용해서 문자열 매칭을 수행합니다. 구체적으로는 문자를 아스키코드 값으로 인식하고 자릿수에 따른 hash 계산을 수행하고 mod 연산한 결과를 사용합니다. 이 값이 일치하면 문자열 비교를 수행해 문자열 매칭이 이루어지는지 확인합니다.
- Hash 값 형성
EX) $h=t_1*10^3 + t_2*10^2 + t_3*10^1 + t_4*10^0$ - 소수를 이용해 mod 연산을 수행합니다.
EX) $value = $ $h$ $mod$ $prime$ - Pattern과 값이 같으면 문자열 매칭 검사를 수행합니다.
$O(n)$의 시간 복잡도가 소모됩니다.
String matching with Finite automata
표를 이용해 문자열 매칭을 수행합니다. State에 따른 전환(transition)이 결정되어 있어 간편하게 문자열 매칭을 수행합니다.
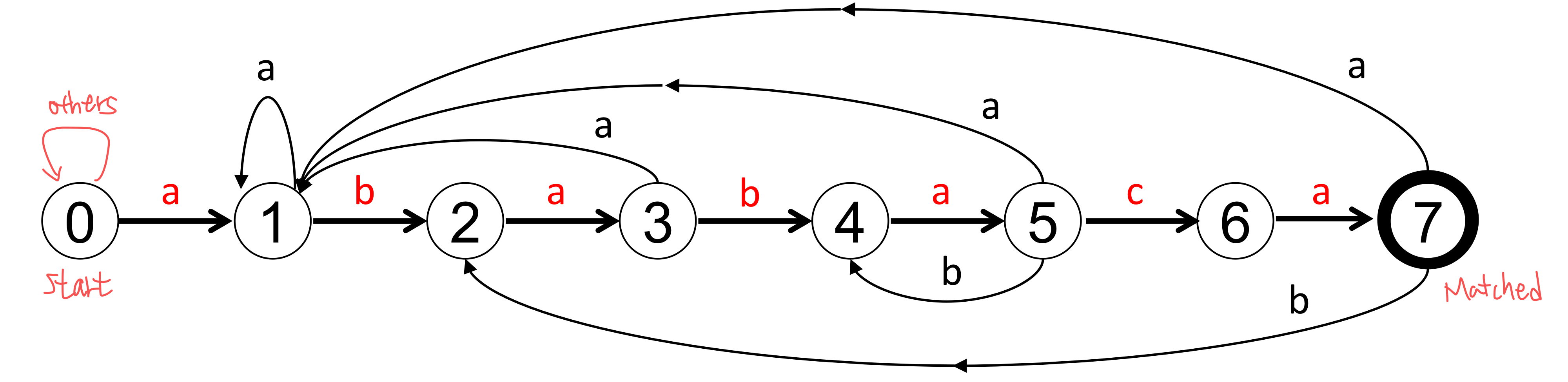
위와 같이 finite automata가 주어지면 다음과 같은 전이 표도 만들 수 있습니다.
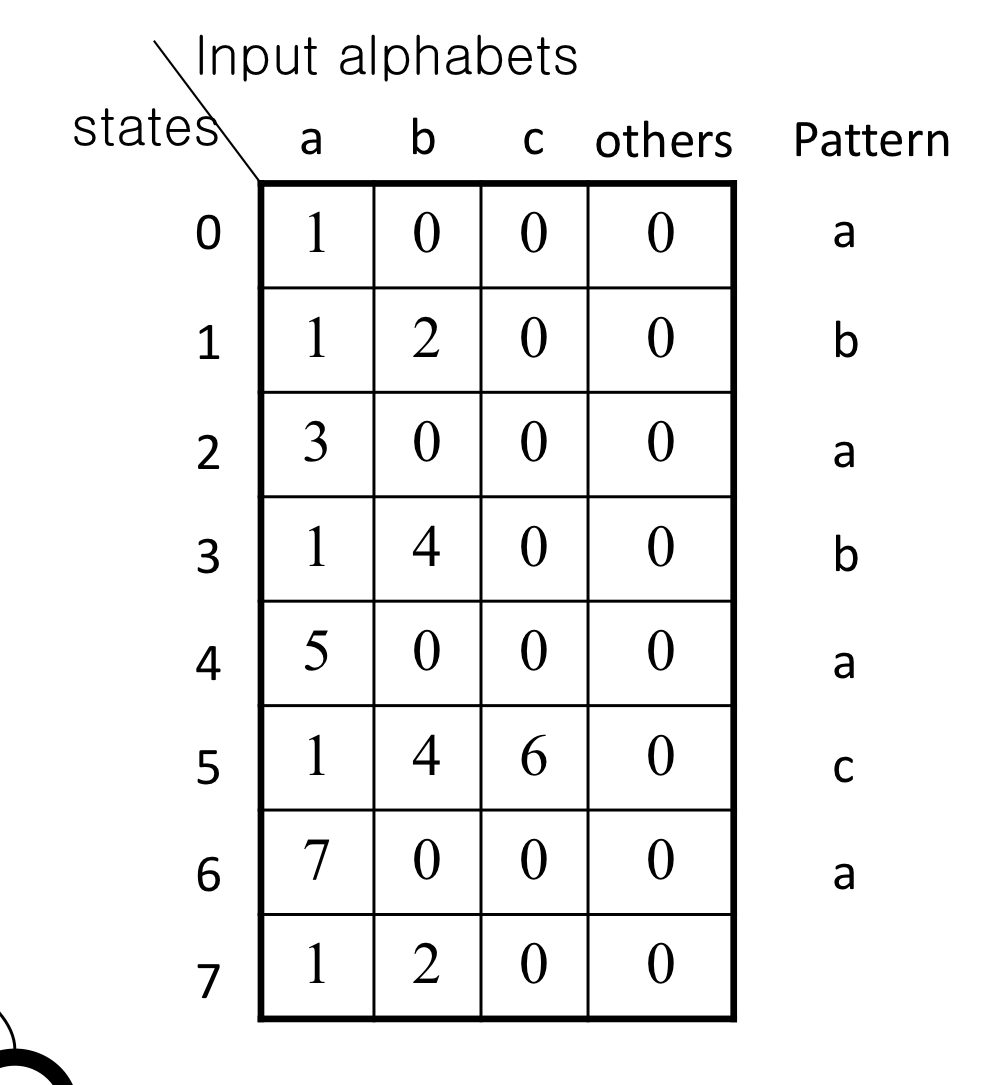
편리하게 문자열 매칭을 수행할 수 있지만, automata를 생성하는 것은 어렵고 오래 걸리는 일이기 때문에 자주 사용되는 방법은 아닙니다. 이 방법 역시 시간 복잡도는 $O(n)$입니다.
Knuth-Morris-Pratt(KMP) algorithm
Prefix와 Suffix를 이용해 문자열 매칭을 수행하는 알고리즘입니다. 만약 pattern에서 prefix와 suffix가 같은 부분이 존재하게 매칭이 실패했다면, pattern을 그만큼 옮기면 되지 않냐가 아이디어입니다.
- Text: B A B A B A A B C B A B
- Pattern: A B A B A C A
위의 예시로 한번 KMP 알고리즘을 수행해보겠습니다. 우선 $\pi$ table을 생성해야 합니다. $\pi$ table이란 prefix와 suffix가 일치하는 경우에 얼마나 일치하는지를 나타내는 표입니다.
| Index | Pattern | $\pi$ |
| 1 | A | 0 |
| 2 | AB | 0 |
| 3 | ABA | 1 |
| 4 | ABAB | 2 |
| 5 | ABABA | 1 |
| 6 | ABABAC | 0 |
| 7 | ABABACA | 1 |
$\pi$ table이 있으면 얼마나 이동할지 이동 경로를 결정할 수 있습니다. 이동 경로는 pattern의 길이 - $\pi$로 결정됩니다.
| Index | Pattern | $\pi$ | 이동경로 |
| 1 | A | 0 | 1 |
| 2 | AB | 0 | 2 |
| 3 | ABA | 1 | 2 |
| 4 | ABAB | 2 | 2 |
| 5 | ABABA | 1 | 4 |
| 6 | ABABAC | 0 | 6 |
| 7 | ABABACA | 1 | 6 |
준비를 마쳤으니, 문자열 매칭을 해보겠습니다.
(1)
B A B A B A A B C B A B
A
(2)
B A B A B A A B C B A B
A B A B A C
(3)
B A B A B A A B C B A B
A B
(4)
B A B A B A A B C B A B
A B A
KMP 알고리즘의 시간 복잡도는 $O(n)$입니다.
Boyer-Moore algorithm
Pattern의 뒷 부분에서 불일치가 일어날 확률이 높은 것을 근거로 오른쪽에서 왼쪽으로 검사하는 방법입니다. 두 가지 heuristic method를 이용해 문자열 매칭을 수행합니다.
- Bad Character Shift
- Good Suffix Shift
Bad Character Shift
2가지 case로 나뉩니다.
1. Bad char가 pattern에 존재하는 경우
가장 오른쪽에 있는 bad char와 위치를 일치시킵니다.
검사를 해보면 다음과 같습니다.
(1)
A B A A D B A B A D B
A A B C D
(2)
A B A A D B A B A D B
A A B C D
또한 이렇게 했을 때, pattern의 이동이 -n이 되는 경우 +1 이동합니다.
(1)
A B A A A B A B A D B
A A B C A
(2)
A B A A A B A B A D B
A A B C A
2. Bad char가 pattern에 존재하지 않는 경우
Pattern의 검사를 bad char 다음부터 진행합니다.
(1)
A B A D A B A B A D B
A A B C A
(2)
A B A D A B A B A D B
A A B C A
Good Suffix Shift
3가지 경우로 나뉘게 됩니다.
1. Good suffix가 pattern 내에 존재하는 경우
Good suffix와 일치하도록 이동합니다.
2. Good suffix의 일부만 pattern에 존재하는 경우
Good suffix와 prefix가 일치하도록 이동합니다.
3. Good suffix가 pattern에 존재하지 않는 경우
Good suffix 이후로 pattern 이동합니다.
만약 Bad character shift 상황이 발생한다면, Bad character shift만큼 pattern을 이동합니다. 그러나 만약 Bad character shift 상황이 아니라면, Good suffix shift의 이동 거리를 구해서 문자열 매칭을 수행합니다.
시간 복잡도는 $O(n/m)$입니다.
정리
| Alg | Time complexity |
| Naive | $O(nm)$ |
| Rabin-Karp | $O(n)$ |
| Finite automata | $O(n)$ |
| KMP | $O(n)$ |
| Boyer-Moore | $O(n/m)$ |
'Study > Algorithm' 카테고리의 다른 글
| 12. Graph Algorithms - Traversal, MST (2) | 2023.06.11 |
|---|---|
| 11. Sort Algorithms (2) | 2023.06.11 |
| 9. Selection(Order Statistics) (0) | 2023.06.08 |
| 8. Search Algorithm (0) | 2023.06.08 |
| 7. Dynamic Programming (0) | 2023.06.08 |
