12. Graph Algorithms - Traversal, MST

Graph Basics

일상의 많은 문제는 Object간의 binary 관계로 이루어져 있습니다. 고속도로나 도시의 지도가 그런 예입니다. 중요한 사실은 이런 binary 관계는 table 형태나 graph 형태로 표현이 가능하다는 것입니다. 그럼 graph 이론을 알고 있으면, 많은 문제에 적용할 수 있다 이말이야

Binary relation represented in tabular form or in grphical form

 

Terminology and Representation

Graph

Directed graph와 Undirected graph, 두 종류로 이루어진다.

Directed graph	Undirected graph
G = (V, E)	G = (V, E)
V : a set of vertices E : a binary relation on V, called edges (= a set of ordered pairs of 2 element from V)	V : a set of vertices E : a set of multisets of 2 elements from V

 

Graph representations

그래프 표현식은 Adjacency matrix → Adjacency lists → Adjacency multi-lists 순으로 발전되고 있습니다.

Adjacency matrix

Adjacency list

Adjacency multi-layer

 

Basic Terminology

Incident

연결된 vertices에 대해서 edge는 incident하다고 한다.

ex) Edge(a,b)는 vertex a와 b에 대해 incident하다.

 

Adjacent

Edge에 의해 연결된 vertices 사이의 관계를 말한다.

ex) Vertex a는 edge(a,b)에 의해서 vertex b와 adjacent하다.

 

Loop

From, into가 incident한 경우이다. ex) Edge(a,a)

Loop case

Subgraph, Spanning

G = (V,E)에 속하는 vertex와 edge로 이루어진 G'을 subgraph라고 한다.

Subgraph

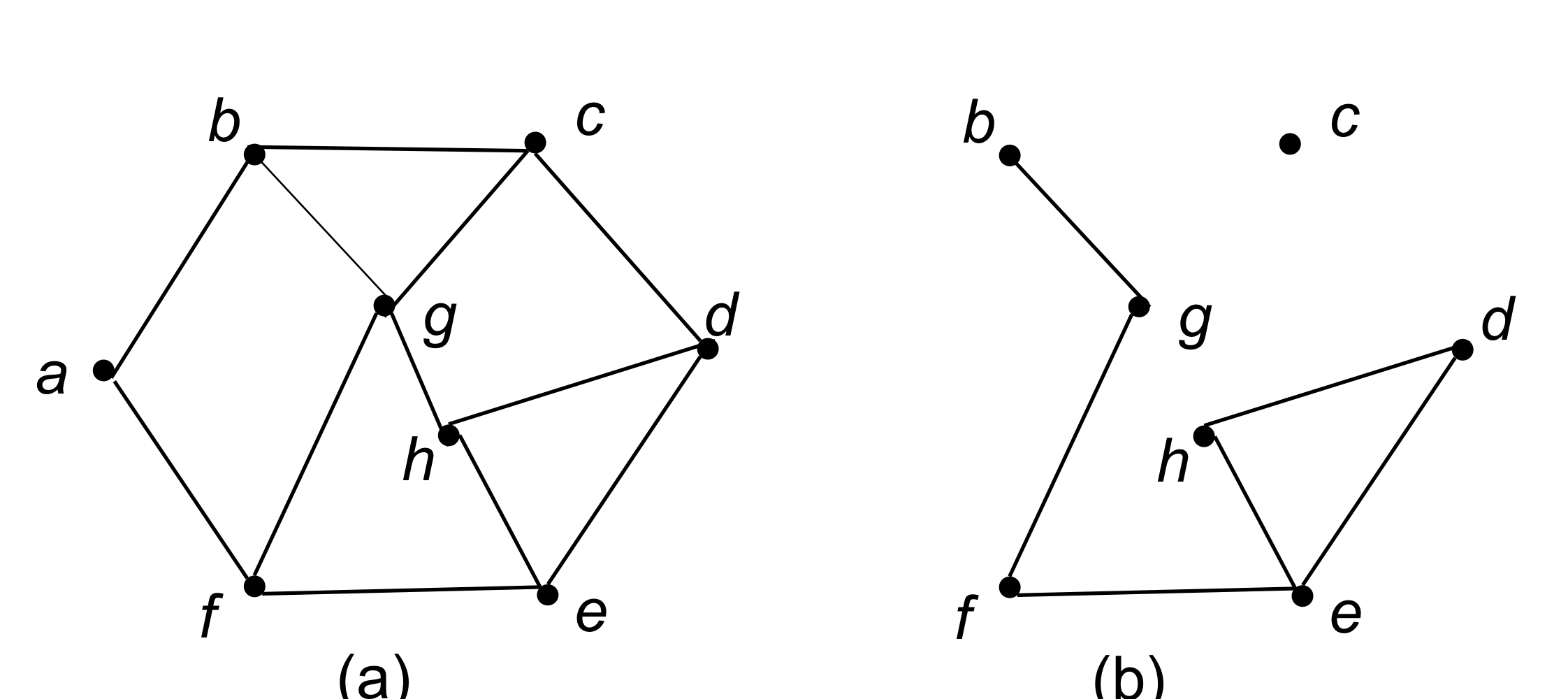
그리고 만약 모든 vertices로 subgraph가 구성되면 spanning이라고 한다.

 

Multigraphs and Weighted graphs

Edge: multiset of Directed multigraph

Directed multigraph G = (V,E)

- E: a multiset of ordered paris from V×V

Multiset이기 때문에 중복이 있어도 상관없다.

 

Weighted graph

Weighted graph는 새로운 notation, f와 g를 이용해 weight를 표현한다. 따라서 G = (V,E,f,g)이다. f는 vertex의 weight를 나타내고 g는 edge의 weight를 나타낸다.

 

Paths

Directed graph에서 path는 edges의 sequence로 나타낸다. $(e_1, e_2, ..., e_n)$

Simple	Elementary
Edge에 중복이 없는 경우	같은 vertex를 다시 방문하지 않는 경우

Example

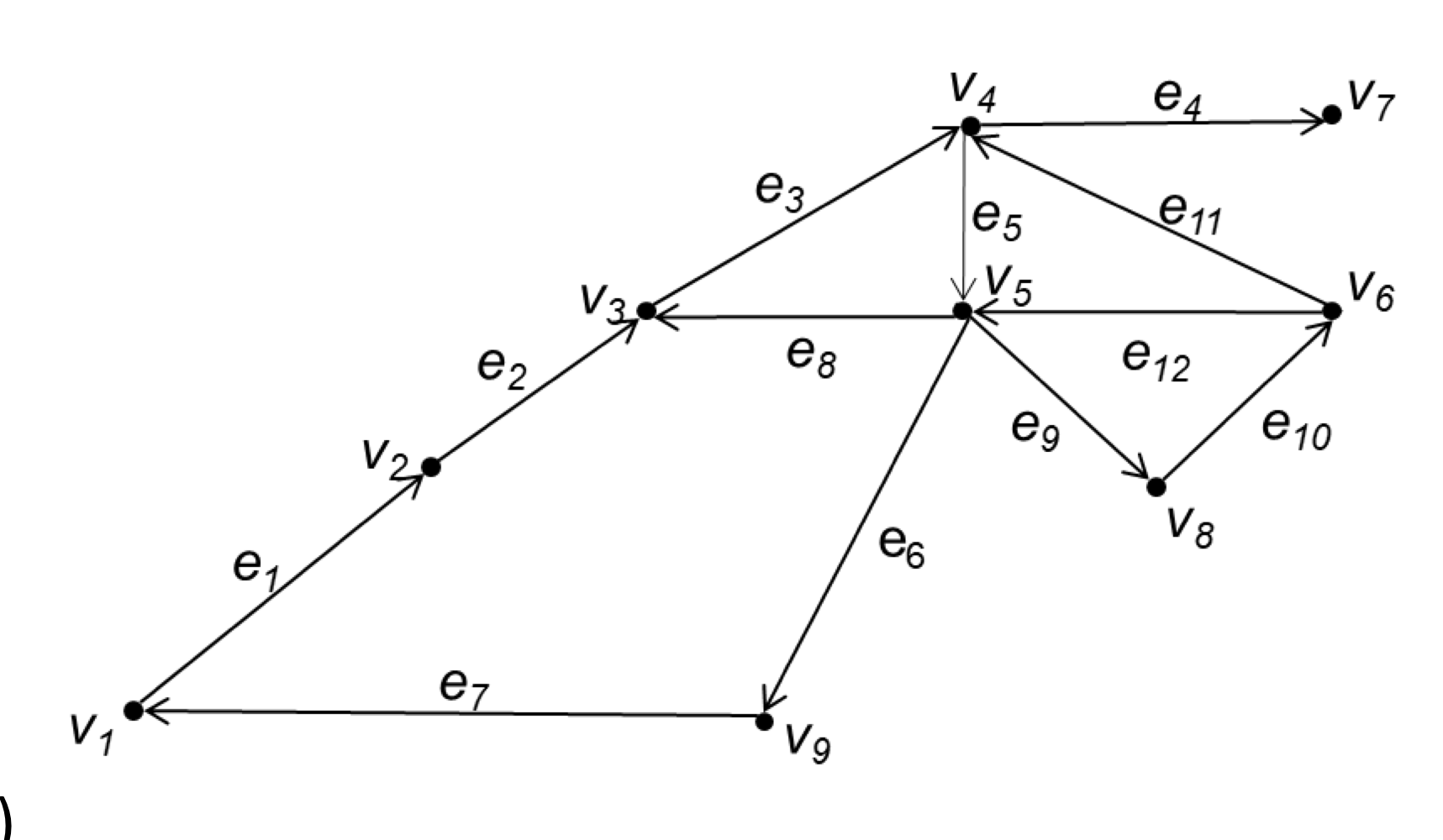
$(e_1,e_2,e_3,e_4)$ : simple, elementary

$(e_1,e_2,e_3,e_5,e_8, e_3)$ : no simple

$(e_1,e_2,e_3,e_5,e_8)$ : simple, but no elementary

 

Circuits

Path가 첫 vertex로 돌아오는 경우 circuit이라고 한다. 마찬가지로 Simple circuit, Elementary circuit이 있다.

 

Data structure: Tree

쉽게 생각해서 spanning graph의 subgraph이다.

 

Definitions

• G : connected, acyclic(no cycles)
• G : acyclic, edge 하나 추가되면 simple cycle이 생김
• G : connected, edge 하나 제거되면 disconnected가 됨
• 두 개의 vertices는 반드시 unique simple path로 connected됨

Conditions

• G : connected, n-1 edges를 가지고 있음
• G : acyclic, n-1 edges를 가지고 있음

 

Data structure: DAG

Directed Acyclic Graph이다. Cycle이 없는 directed 그래프라는 뜻이다. Partial order를 가지는 경우 modeling하기에 좋은 자료구조이다. 쉽게 말해서 a→b, b→c와 같은 부분적인 구조를 가지고 있을 때 적합한 그래프이다.

DAG example

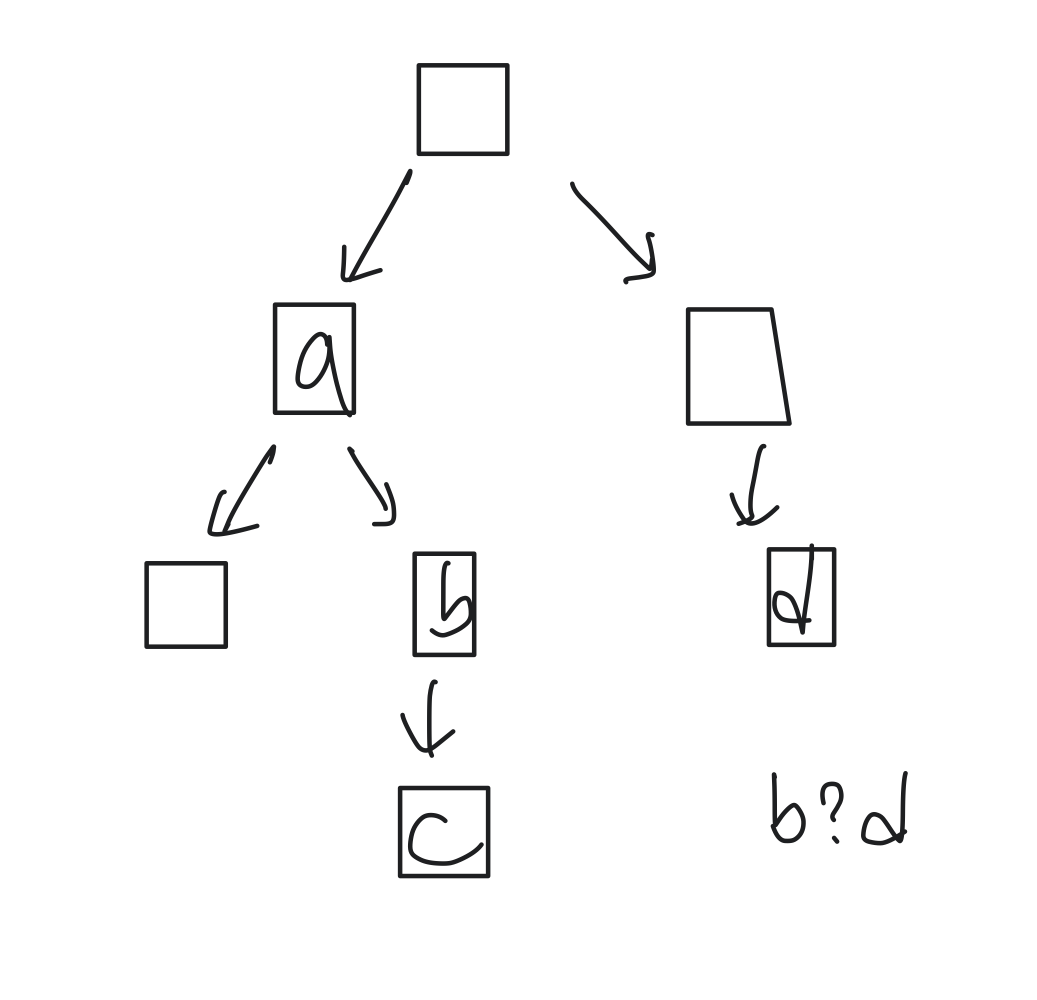
a→b, b→c와 같은 order를 가지면 우리는 a→c라는 것을 알 수 있다. 이렇게 부분 task를 정렬하는 것을 topological ordering(sorting)이라고 한다.

 

Topological Ordering

우리가 옷을 입는다고 생각해 볼 때, 속옷을 입고 겉옷을 입으며, 양말을 신고 신발을 신는 등의 고정된 부분 순서가 있을 것이다. Topological ordering은 그런 선후 관계를 기반으로 process를 순서대로 정렬하는 알고리즘이다. 

 

만약 우리가 다음의 일 처리 과정을 가지고 있다고 생각해보자.

순서대로 한줄로 배열하고 싶음

그럼 알고리즘의 진행과정은 다음과 같다.

Topological ordering

그럼 결과물은 다음과 같이 나온다.

Result

 

Traversarl Algorithm

Graph의 모든 vertex를 방문하기 위한 알고리즘이다. DFS와 BFS가 있다.

 

Depth First Search(DFS)

계속해서 방문할 수 있는 노드를 방문하다가, 더 이상 방문할 노드가 없으면 이전에 방문했던 노드로 돌아가는 알고리즘이다. 계속해서 반복하다 보면, 모든 노드를 방문하게 된다.

DFS algorithm

 

그림으로 보면 이해하기 쉽다.

Graph

방문할 수 있는 노드가 더 이상 없다.

방문할 노드가 남아있는 vertex까지 돌아와서 방문할 수 있는 vertex를 방문한다.

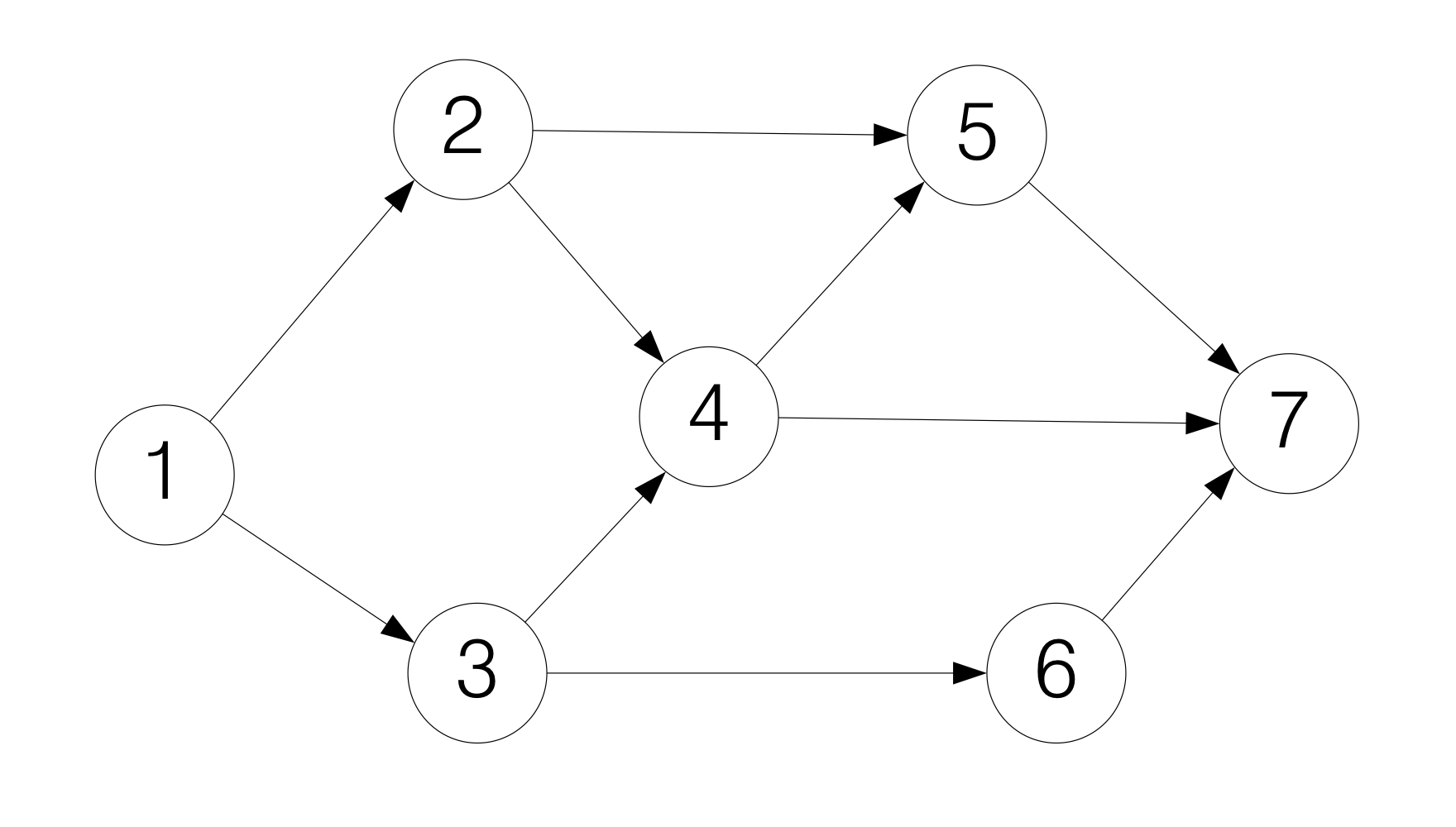
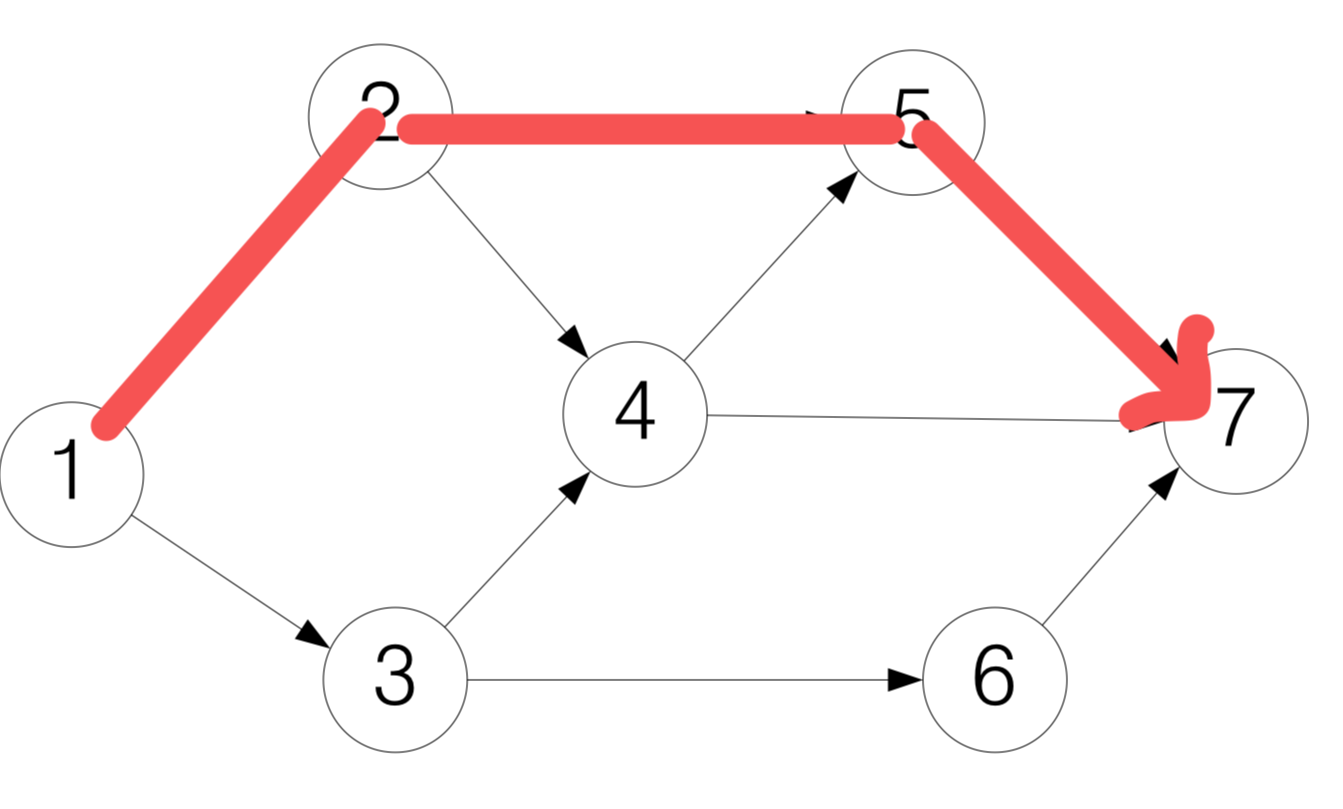
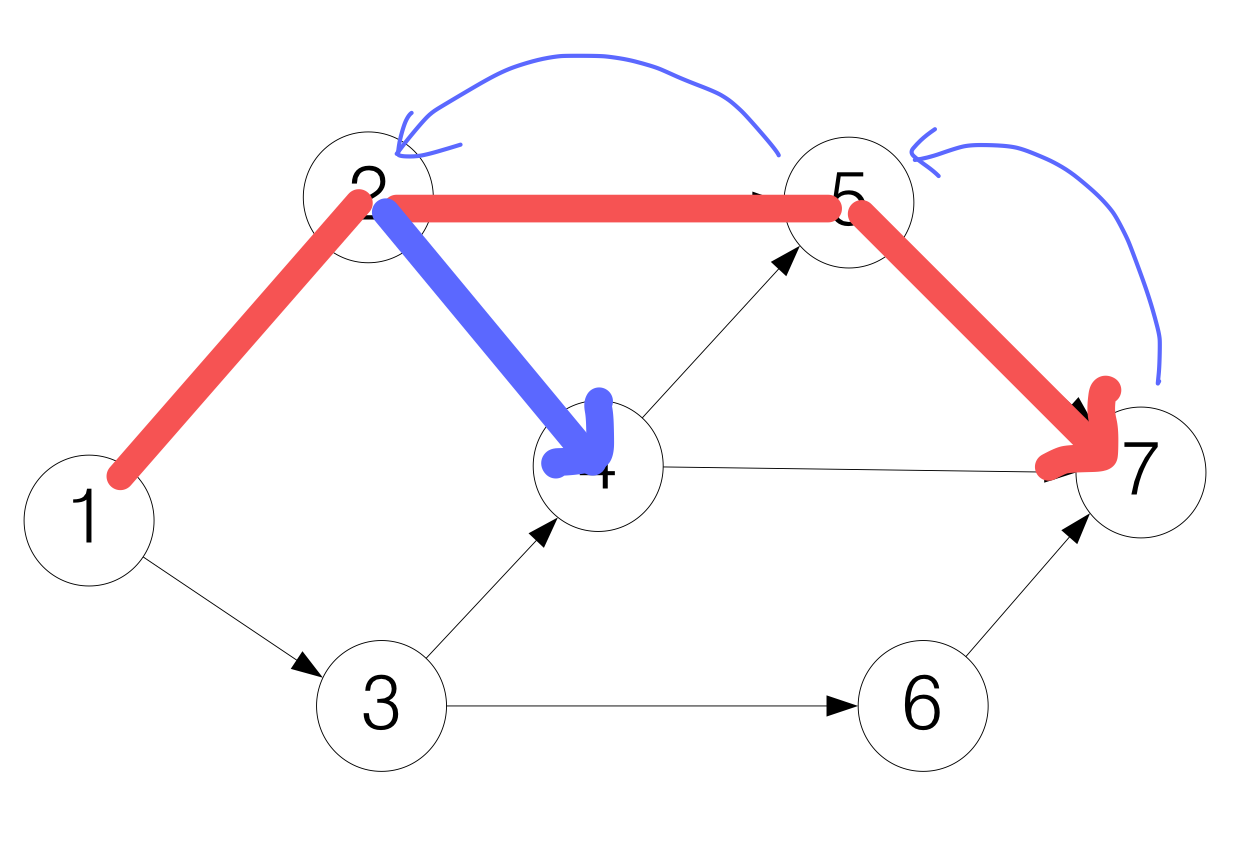
이런 식으로 모든 노드를 방문하게 된다. 보면 알겠지만, 최대한 깊게 탐색을 해서 depth first라는 이름이 붙게 된다. 또한 구조를 고려해보았을 때, stack을 이용하면 효과적으로 알고리즘을 구현할 수 있다. (Stack: Frist in, Last out)

 

Topological sort에도 적용하여 사용할 수 있다.

Socks, Shorts, T-Shirt, Batting glove 중 탐색을 시작하면 된다.

 

Breadth First Search(BFS)

DFS가 그러했듯이, BFS의 이름을 보면 너비 우선 탐색이라는 것을 알 수 있다. Root부터 방문할 수 있는 모든 child vertex를 방문한다. 이를 반복해서 모든 노드를 방문할 수 있다. DFS가 stack에 적합하듯이 BFS는 queue에 적합하다. (Queue: First in, First out) 그냥 방문하는 노드 다 집어 넣고, 모든 child를 방문하면 parent node를 pop하면 된다.

 

알고리즘은 다음과 같다.

BFS algorithm

진행과정은 따로 해보지 않겠다.

 

Minimum Spanning Tree

Spanning tree를 만들 건데, edge의 weight 합이 제일 작게 만드는 알고리즘이다. MST는 생각보다 많은 곳에서 사용된다. 교수님이 좋아하신다.

MST

합으로 구하는 것이기 때문에, edge의 weight가 동일한 것이 있으면 MST는 unique하지 않는다. MST를 만들어 주는 몇 가지 알고리즘이 있다.

 

Prim's algorithm

간단하게 생각해서 greedy하게 smallest weight를 가지는 edge를 선택하는 알고리즘이다. 아무거나 root로 잡고 current tree의 weight 합이 최소가 되도록 edge를 선택해 tree를 키워나간다.

Prim's algorithm

구체적인 알고리즘은 다음과 같다.

Prim's algorithm

시간 복잡도를 구해보자면, 

우선 heap을 사용한다고 가정한다. Heap을 사용하면 min 값을 $O(1)$에 찾을 수 있고, update하는데 $O(log|V|)$의 시간이 소모되기 때문이다.

 

그래서 모든 edge를 보고 $d$를 update한다고 생각하면, $O(|E|)$×$O(log|V|)$의 시간이 소모된다. 따라서 전체 시간 복잡도는 $O(|V|) + O(|E|)O(log|V|)$가 되어 $O(elogn)$이 된다.

 

*Heap이 아니라 Finbonacci heap을 이용하면 $O(|E|+|V|log|V|)$로 시간 복잡도를 더 줄일 수 있다. 보통 $|E|>|V|$이다.

 

다음으로 Correctness를 증명해본다.

$e_1$은 smallest weight을 가진다.

 

Kruskal's algorithm

Prim과 마찬가지로 greedy approach이다. Edge의 모든 weight를 정렬하고 작은 edge부터 MST에 포함하는 방법이다. 물론 cycle이 생기기 전까지만 수행한다.

Example of Kruskal's algorithm

알고리즘은 다음과 같다.

Kruskal algorithm

Tree의 depth가 큰 쪽으로 UNION되며, balancing tree를 유지한다. 시간 복잡도는 $O(elogn)$이다. 또한 correctness 증명법은 Prim과 같다. Contradiction을 이용해 증명한다.

 

Bound on MST problem

MST 문제의 시간 복잡도 범위는 다음과 같다.

 

Upper Bound: $O(elogn)$

Lower Bound: $\Omega(e)$

 

*Euclidean MST라면 $O(nlogn)$도 가능하다.

Prim에 Fibonacci heap을 이용하면 $O(e+nlogn)$이었다.

Euclidean 거리가 매우 큰 경우에 MST에 포함되지 않기 때문에 |E| 지울 수 있게 된다.