1. Policy Iteration
초기 Policy에서 시작해서 Policy Evaluation, Policy Improvement를 반복하여 Optimal policy를 찾는 방법이다.
1.1. Policy Evaluation
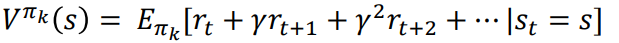
$Q^{\pi}(s,a) = R(s,a) + \gamma \sum_{s'}p(s'|s,a)V^{\pi}(s')$
$V^{\pi}(s) = \sum_{a} \pi(a|s)Q^{\pi}(s,a)$
State-value function이 $V_{\pi}$수렴할때까지 계속 evaluate하거나, 한번만 하고 Policy Improvement로 넘어가도 된다.
1.2. Policy Improvement (control)

$Q^{\pi}(s,a) = R(s,a) + \gamma \sum_{s'}p(s'|s,a)V^{\pi}(s')$
$V_{\pi}$를 이용해 $Q$를 최대로 하는 action을 선택해 Policy를 업데이트한다. Policy Improvement로 $\pi$가 더 이상 업데이트되지 않는다면, $\pi_{c}$는 다음의 Bellman Optimality Condition을 만족한다. 그러므로 이때의 policy가 optimal policy, $\pi^{*}$이다.

1.3. 분석
위 Iteration의 결과는 다음의 관계성을 가짐으로 optimal에 가까워진다.

2. Value Iteration


위 식을 반복적으로 계산하여, $V^{*}$를 구한다. 명확한 policy를 구하는 것은 아니지만, 따로 best action을 저장한다면 optimal policy를 구할 수 있다. $O(|A||S|^{2})$의 시간복잡도가 소요된다.
3. Variants of DP
지금까지의 DP 방법은 synchronous backup을 이용해, iteration에서 모든 상태를 병렬로 업데이트했다. 계산량이 엄청나다. Asynchronous DP는 각 state를 순서에 상관없이 업데이트하여 계산량을 감소시킬 수 있는 장점이 있다.
- In-place dynamic programming
- Prioritized sweeping
- Real-time dynamic programming
3.0. Synchronous value iteration
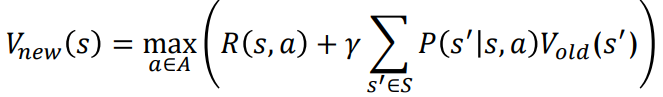

Asynchronous DP보다 저장을 1번 더 하는 단점을 가지고 있다.
3.1. In-place dynamic programming

In-place 형식으로 계산을 한다.
3.2. Prioritized Sweeping

$V_{old}$와 $V_{new}$의 차이가 큰 state부터 업데이트하는 방식이다.
3.3. Sample Backups
모든 state와 action을 가지고 계산하지 않고, sampling을 통해 계산하는 방법이다. Model-free일 때, 주로 사용한다.
3.4. Approximate DP
Value function을 Function Approximator $\hat{V}(s,\omega)$로 계산하는 방법이다. 주로 Value function이 계산하기 어려울 때, 이와 같은 방법을 사용한다. 계산 방법은 같다.
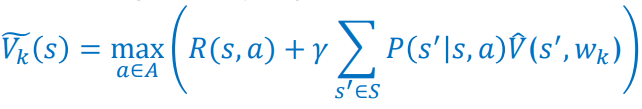
'Study > Reinforcement Learning' 카테고리의 다른 글
| [project] QMIX review (0) | 2023.05.01 |
|---|---|
| 4. Monte Carlo Methods and Temporal Difference Learning in Policy Evaluation (0) | 2023.05.01 |
| 2. Bellman equation and MDP (0) | 2023.05.01 |
| 1.Introduction (0) | 2023.05.01 |
