3. Recursion

만약 어떤 문제가 작은 문제들로 나누어질 수 있다면, 이 문제는 recurrence relation으로 해결할 수 있습니다. 이 방법을 'Divide-and-conquer'라고 합니다.

 

Recurrence Relation

다음의 특징을 가지고 있습니다.

• $a_n$이 $a_i$, $a_j$.. 등과 같이 표현되는 경우 (i, j < n)
• Boundary condition
  계산이 시작될 수 있게 해주는 하나 이상의 값들
• Example
  $a_0$ = 1, $a_1$ = 1
  $a_n$ = $a_{n-1}$ + $a_{n-2}$

 

대표적인 예시로는 Factorial, Fibonacci number가 있습니다.

 

Example : Factorial

팩토리얼은 다음과 같이 정의됩니다.

 

$n! = n*(n-1)*(n-2)*...*2*1$

 

이를 recurrence relation으로 표현하면 다음과 같습니다.

Factorial

 

이 함수의 correctness는 다음과 같이 증명할 수 있습니다.

Correctness of factorial

 

그리고 이를 알고리즘으로 표현하면 다음과 같이 나타낼 수 있습니다.

Factorial algorithm

 

Time complexity를 구해야 하는데, 기존처럼 instrution을 하나하나 따라가는 것은 불가능해 보입니다. 우선은 간단하게 다음과 같이 표현할 수 있습니다.

Time complexity

 

Recurrence relation을 가지는 알고리즘의 time complexity를 해결하는 방법은 크게 3가지가 있습니다.

• Substitution method
• Recursion-tree method
• Master method

 

Substitution method

가정을 하는 방법입니다. 알고리즘이 대충 O(logn)이라고 가정하고 mathematical induction을 이용해 이를 증명합니다.

 

이 방법이 효과적이기 위해서는 good guess를 하는 수밖에 없습니다.

 

EXAMPLE

위와 같은 관계가 있을 때, 우리는 다음의 가정을 해볼 수 있습니다.

Mathematical induction을 이용해 이를 증명합니다.

Mathematical Induction

 

Recursion-tree method

Recursion tree를 그리고 time complexity를 계산하는 방법입니다.

 

EXAMPLE

이 경우 tree를 그려봅니다.

Recursion tree

 

Tree의 height를 구하고, 각 node의 time complexity를 모두 더해줍니다.

이렇게 해서 우리는 알고리즘의 time complexity가 $O(n^2)$임을 알 수 있습니다.

 

Master method

가장 편리한 방법으로, recurrenc relation이 가지는 관계의 정형화된 구조를 바탕으로 time complexity를 구하는 방법입니다. 구조는 다음과 같습니다.

 

$T(n) = aT({n \over b}) + f(n)$

a ≥ 1, b > 1, f(n) is an asymptotically positive

 

a와 b의 관계를 통해 T(n)을 구할 수 있습니다.

• $a>b^k$  T(n) ∈ $\Theta (n^{log_b a})$
• $a=b^k$  T(n) ∈ $\Theta (n^{k}log n)$
• $a<b^k$  T(n) ∈ $\Theta (n^{k})$

 

EXAMPLE

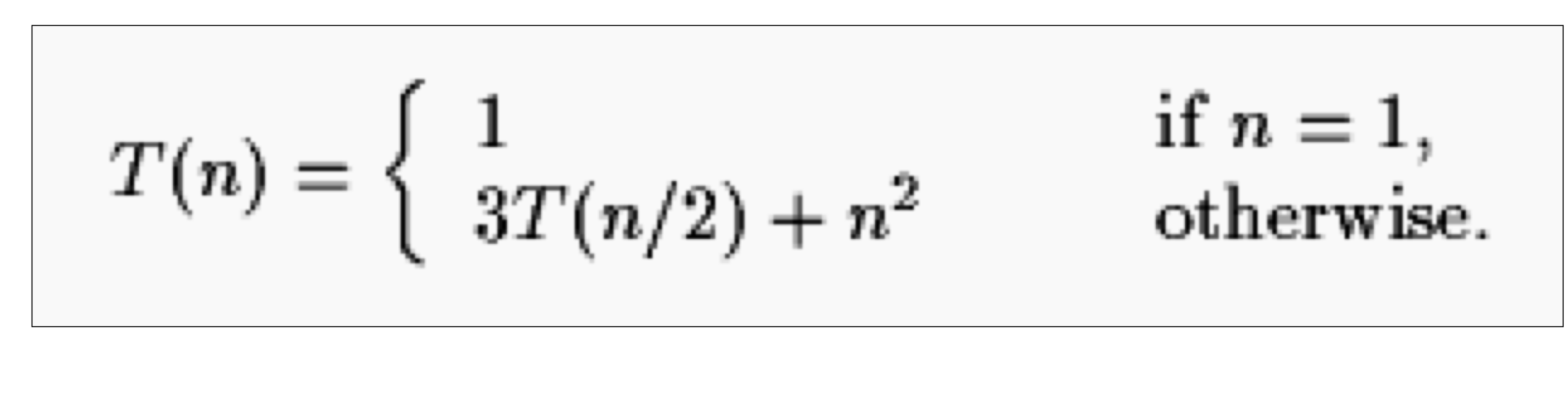
a = 3, b = 2, k = 2이기 때문에 case 3이 되어 T(n)은 $\Theta(n^2)$이 됩니다.

 

Problems with Recursion

Computation of Fibonacci 5

반복해서 계산되는 경우가 많기 때문에 exponential time이 걸리게 됩니다. 이를 해결하기 위해 Memoization 방법을 사용합니다. 다음포스팅에서 다루겠습니다.

 

Recursion v.s. Iteration

Recursion(left) / Iteration(right)

Recursion과 Iteration은 언제나 상호 간의 전환이 가능합니다. Recursion은 Top-down method이고 Iteration은 Bottom-up method이기 때문입니다.