Greedy Algorithm
우리가 결정을 내릴 때, 현 상태에서 제일 좋은 결과(=locally best)를 선택하는 알고리즘입니다. 많은 경우에 Global optimal solution이 아니기 때문에 사용이 제한적이지만, Greedy algorithm으로 global optimal solution이 나오는 경우나 여러 제약으로 인해 optimal solution을 찾는 것이 불가능한 경우에 사용되는 알고리즘입니다.
Returning changes
우리에게 k 코인이 있을 때, 최대한 적은 수의 코인으로 교환해 준다고 생각해 봅시다. [quarter(25c), dime(10c), nickel(5c), penny(1c)]

총 6개의 코인으로 교환해줄 수 있습니다.
항상 optimal solution이 되지는 않습니다. 가령 코인의 단위가 [big(11c), mid(5c), small(1c)]라고 가정해 봅시다.
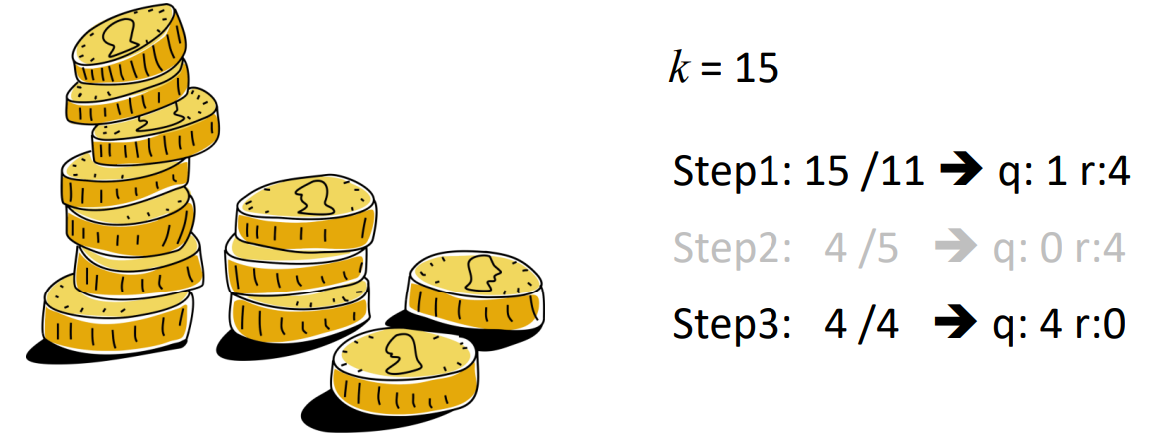
Greedy 하게 선택하는 경우 총 5개의 코인으로 교환을 하게 됩니다. 하지만 optimal solution은 되지 못합니다. Mid 3개로 교환하는 것이 optimal 하기 때문입니다.
Scheduling
하나의 미팅룸을 가지고 있고 다음처럼 request가 있다고 생각해 봅시다. 가장 많은 request를 처리하기 위해서 어떻게 해야 할까요?
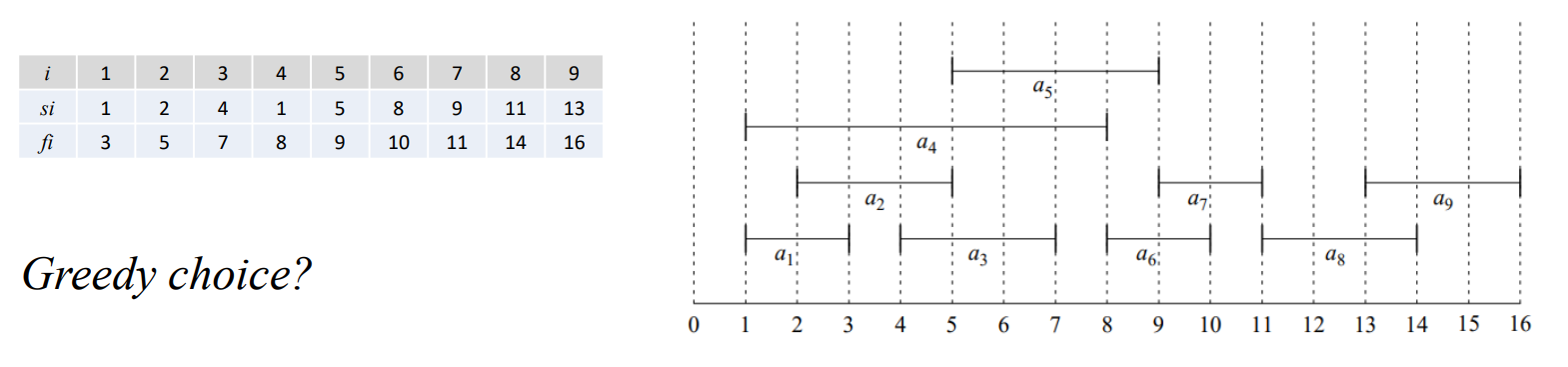
이용시간이 짧은 request부터 선택하는 것이 올바를까요? (이 경우에는 짧은 것부터 처리하는 것이 맞습니다.) Greedy 하게 선택을 한다 해도 무엇이 최선인지 명확하지 않습니다. 다음은 몇 가지 방법입니다.
Design Strategy: Greedy Algorithm
- 문제의 Optimal substructure 찾기
- Recursive solution 구하기
- Greedy choice가 하나의 subproblem인지 보이기
- 항상 Greedy choice가 가능한지 보이기
- Recursive algorithm 만들기
- Recursive algorithm을 Iterative algorithm으로 바꾸기
Divide-and-Conquer
문제를 Subproblem으로 나누고 subproblem을 해결함으로써 문제를 해결하는 방법입니다. 문제를 나누는 일은 자기 마음대로 하면 됩니다. 대표적인 예시로는 Merge sort나 Binary search 등이 있습니다.
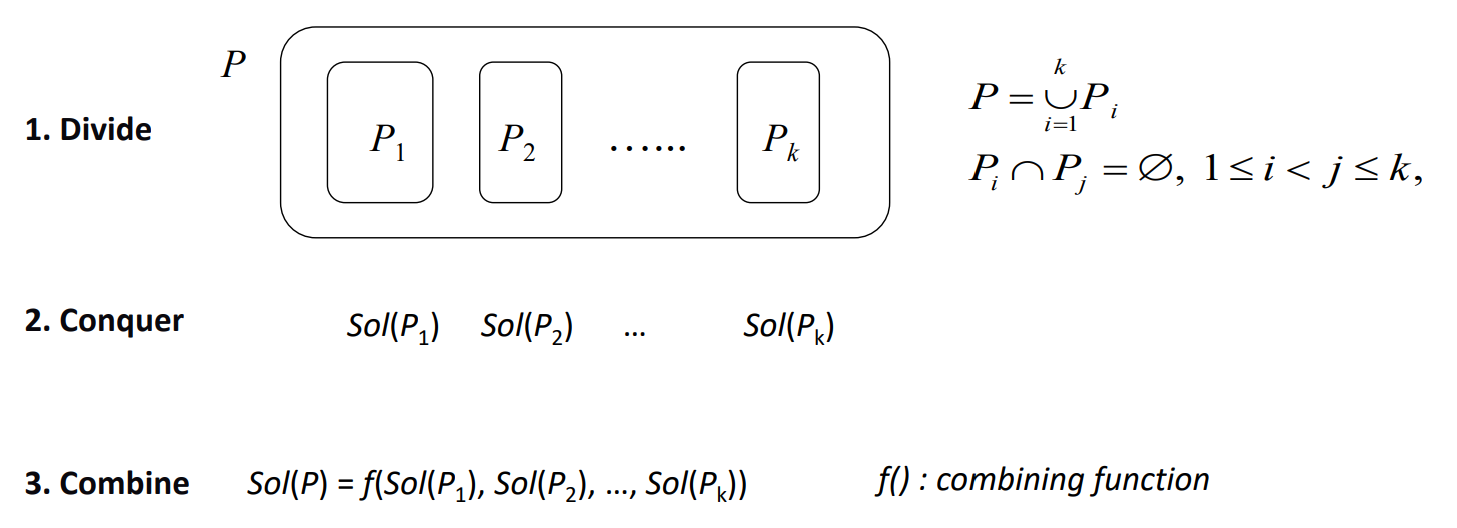
Time complexity는 다음과 같습니다.
$T(n) = T(n_1) + ... + T(n_k) + M(n)$
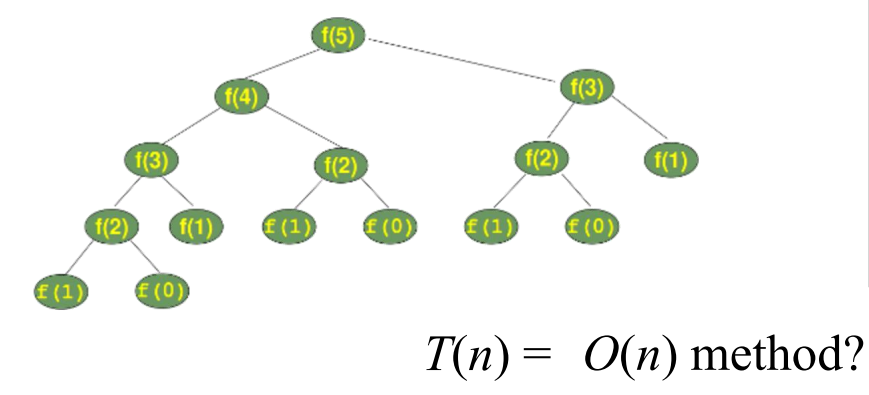
Fibonacci number
시간 복잡도를 구해 봅시다.
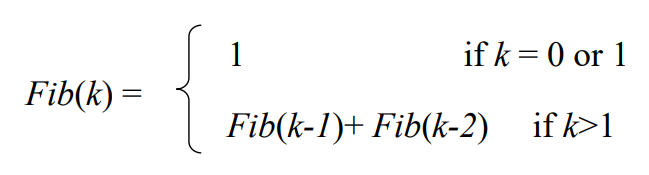
$T(n) = T(n-1) + T(n-2) + O(1)$
$> 2T(n-2)$
$> 2*2T(n-4) $
$> ... > 2^{{n \over 2}}T(0) = 2^{{n\over2}}$
따라서 $T(n) = O(2^{n})$가 됩니다.
*$T(n)=O(n)$도 Memoization을 사용하면 가능합니다. 오래 걸리는 이유가 반복되는 계산이 많기 때문입니다.
Matrix multiplication
...
'Study > Algorithm' 카테고리의 다른 글
| 8. Search Algorithm (0) | 2023.06.08 |
|---|---|
| 7. Dynamic Programming (0) | 2023.06.08 |
| 5. Amortized Analysis and Adversary Argument (0) | 2023.06.08 |
| 4. Probabilistic Analysis and Randomized Algorithm (0) | 2023.06.08 |
| 3. Recursion (0) | 2023.06.08 |
