Physical memory에 virtual memory를 할당시켜 보려는 노력을 계속했었는데, contiguous한 성질 때문에, fragmentation이라는 한계에 부딛히게 된다. 이를 해결하고자 도입한 것이 paging이다. 아이디어는 간단하다. 메모리를 fixed-sized page로 잘게 나눠버리는 것이다. (보통 4KB)
Translation (VA->PA)

방법은 기존과 동일하다. Logical address에서 일정 top bit로 table에 저장되어 있는 내용을 참고해 physical frame number를 찾고, offset만큼 이동해 데이터를 참조하게 된다. 실제 동작은 다음처럼 진행된다.

Page Table
Mapping 정보가 저장된 table이다. 프로세스마다 1개씩 가지게 된다. Page table은 메모리에 저장되며, 하나의 row는 page table entry라고 한다. 크기를 계산해보면 대충 다음과 같다.
- 상황
- 32-bit address space
- 4 KB pages
- 풀이
- Page table entry size = 32bit -> 4 byte
- Page table size = # entires * size of entry
- # of entries = # virtual pages = 2^(bits for VPN)
- Bits for VPN = 32 - page offset = 32 - log(4KB) = 20
- Page table size = 2^20 * 4 bytes = 4 MB
(2^20 = 1MB)
Context switch가 일어나면, page table base register를 PCB에 저장하게 된다.
Page table에는 VPN->PPN 외에도 valid bit, protection bit, present bit, reference bit, dirty bit이 저장되어 있다.
Memory accesses with pages
다음의 명령어와 page table을 가정해보자.

- 0x0020; movl 0x1100, %edi
- Page table 위치: 0x5000
실제로 일어나는 일련의 과정은 다음과 같다.
- Page table 접근, VPN 0에 해당하는 PPN 찾기
- 0x5000으로 이동 (메모리 접근 1회)
- VPN 0 -> PPN 2임을 깨달음
- 메모리 0x2020으로 접근 (메모리 접근 2회)
이처럼 paging을 이용해 메모리 접근을 수행할 경우, 1회 메모리 접근에 실제로는 2번이나 접근학게 된다. 이렇게 되면 컴퓨터의 메모리 접근 속도는 2배가 되어 매우 느려지게 된다.
Advantages of Paging
- Fragmentation이 없음
- 빠르게 allocate, free 가능함
- Swap이 간단해짐(disk에 있을래, memory에 있을래)
Disadvantages of Paging
- Internal fragmentation 발생: 5KB segment 저장시 4KB page 2개가 필요해짐
- Page table 추가적인 접근 발생 -> TLB로 해결
- Page table 추가로 저장해야함
메모리 접근 과정을 다시 생각해 보면, 시간 소모가 큰 PTE 접근만 어떻게 해결해 보면 될 것 같다. Cache의 개념을 차용해 Translation Lookaside Buffer(TLB)를 이용한다.
TLB

HW로 구현된 일종의 address translation을 위한 CPU 케시이다. Fully associative일 때, 위와 같은 bit 구분을 가지고 있다. Two-way, four-way associative도 가능한데, 이 경우에 tag에 %num_set을 수행한 결과가 set 위치라고 생각하면 된다.

Direct map의 경우 PTE와 같다고 생각해도 된다. Assocative하게 구현하는 데는 장단점이 있다.
| Higher associativity | Lower associativity |
| + Better utilization + Fewer collisions - Slower - More HW |
+ Fast + Simple + Less HW - Greater chance of collisions |
TLB performance
TLB는 TLB miss rate로 평가된다.
# TLB misses / # TLB lookup

위와 같은 코드의 경우 # TLB lookup은 2048회이다. # TLB miss는 page의 크기가 4KB, sizeof(int)가 4B이므로, 하나의 페이지에 1024개의 int를 접근할 수 있다. 2048 접근이 이루어졌기 때문에 2회 TLB miss가 발생함을 알 수 있다. 따라서 TLB miss rate는 2/2048 = 0.1%가 된다.
이를 통해 page의 크기가 작아질 수록 miss rate가 커짐을 알 수 있다. 성능을 높이고 싶으면 page size를 키우면 된다. 또한, page size만큼 데이터 접근이 용이함으로 sequential array같은 데이터에 유용함을 알 수 있다.
특정 작업에 용이한 performance를 보이기 때문에, 여러 workload에 대해 TLB 성능을 평가하게 된다. 그리고 이는 우리가 아는 cache locality가 많이 고려된 내용이다.
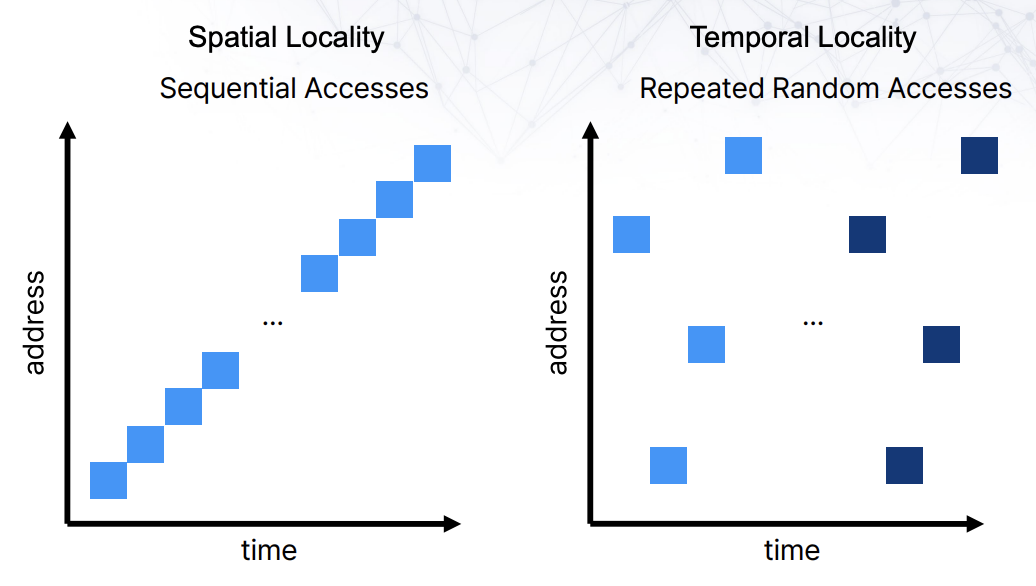
이런 workload에서 좋은 performance를 얻기 위해서는 replacement policy를 잘 만들면 된다. TLB miss가 발생할 때마다, 페이지 업데이트를 진행한다면 sequential locality에 대해서 좋은 성능을 보이겠지만, repeated random access에 대해서는 아주 안좋은 성능을 보일 것이다.
TLB Replacement Policies
많은 방법이 있지만, 대표적으로 LRU와 Random을 살펴본다.
- LRU(Least Recently Used): 가장 최근에 덜 사용된 친구 evict
- Random: 아무거나 evict
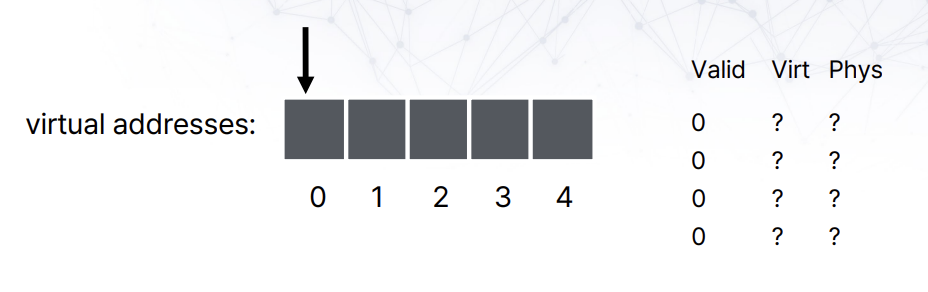
TLB entry는 4개인 반면, page는 5개의 TLB tag를 가지고 있다. 이 경우 LRU를 사용하며 page tag가 0-1-2-3-4-5를 반복한다면, tag 5가 참조될때부터 계속해서 miss가 발생하게 된다. 매우 특별한 케이스긴 하지만, 실제로 이런 경우가 많이 발생하며, 차라리 random이 더 좋은 경우가 많고, 실제로 몇 TLB는 random eviction을 채택해 사용하고 있다.
Context Switches with TLB
다른 프로세스에서 TLB entries를 공유해서 사용하고 싶은 경우가 있을 수 있다. Context switch가 발생할 때마다, TLB를 지워버리는 방법도 있겠지만, 비용이 너무 많이 든다. 차라리 TLB entry에 이 TLB가 어느 프로세스의 TLB인지 명시하는 편이 더 효과적이다. 이를 위해 TLB entry에 8 bits를 할당해 프로세스를 식별하는 방법, ASID(Adress-Spaced IDentifier)가 있다.
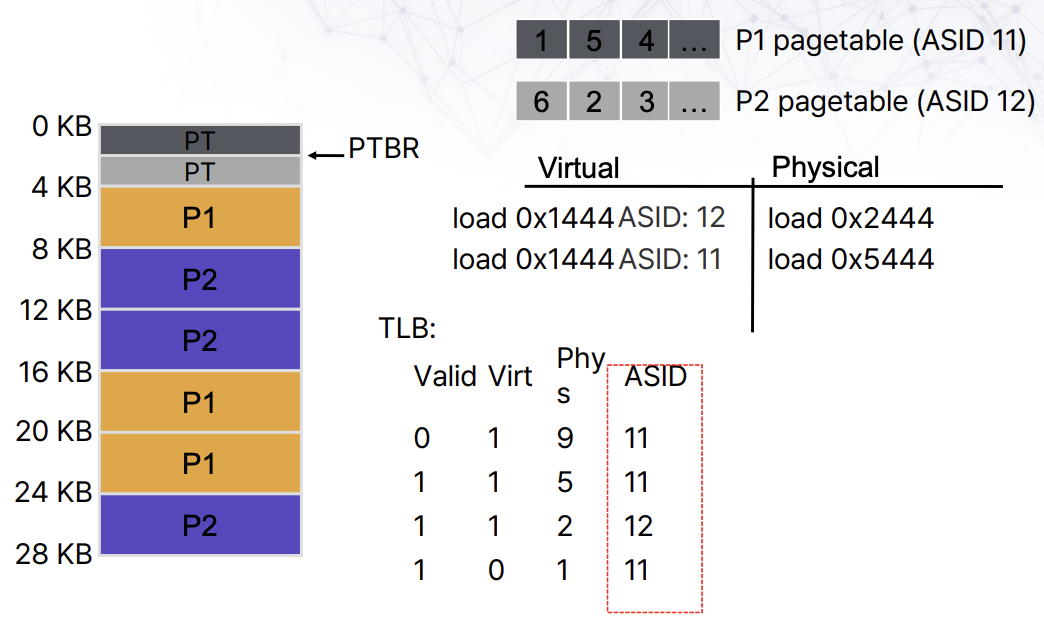
Context switch가 매우 큰 비용소모를 조장하기 때문에, ASID같은 방법을 사용하는 것인데, 다른 프로세스의 악의적인 행위에 대한 방어체계가 없는 등 감염될 문제를 가지고 있다. 그래서 여러개의 TLB를 사용해 관리하기도 한다.
Page Table Size
Page table의 크기를 계산해보면, 뭐 살짝 추가만해도 겁나 커지게 된다.
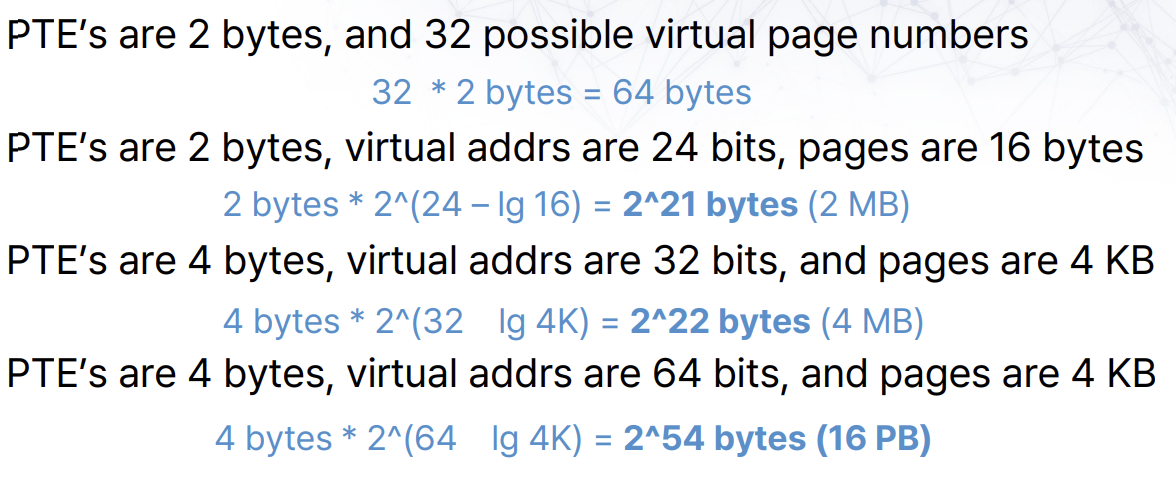
그 이유는 사용하지 않는 부분까지 Virtual memory address와 Physical memory address를 mapping하고 있기 때문이다. 이런 simple linear page table을 사용하지 않으려고 여러 방법이 제안되었다.
- Inverted page table
- Segmented page table
- Multi-level page table
Inverted page table
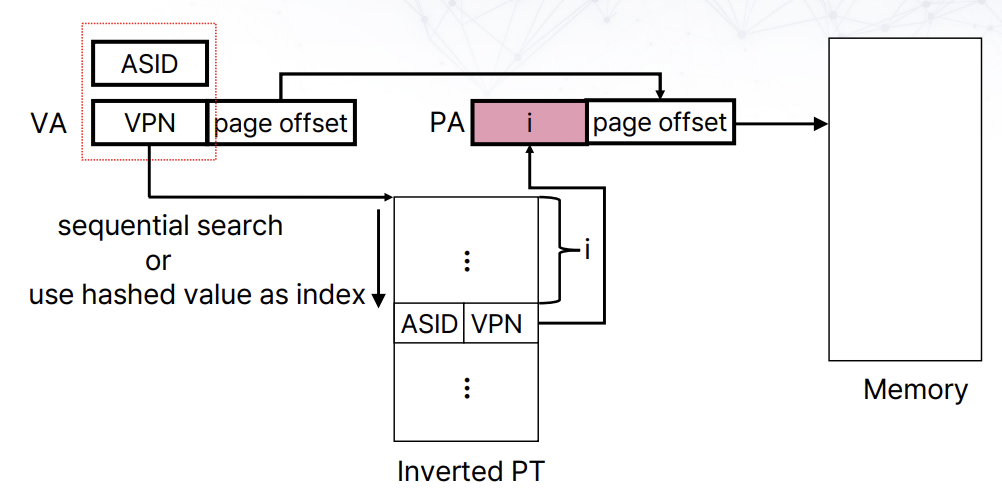
나이브한 접근으로 valid physical mapping에 대해서만 virtual pages를 관리하는 것이다. Physical address를 찾기 위해 hash(ASID+VPN)을 통해 PA를 계산한다.
Hash를 사용함으로써, 적은 수의 bit만 검사할 수 있다는 장점이 있다. 또한 valid PM만 mapping되어 있기 때문에, 검색 시간이 줄어들게 된다.
Segmented page table
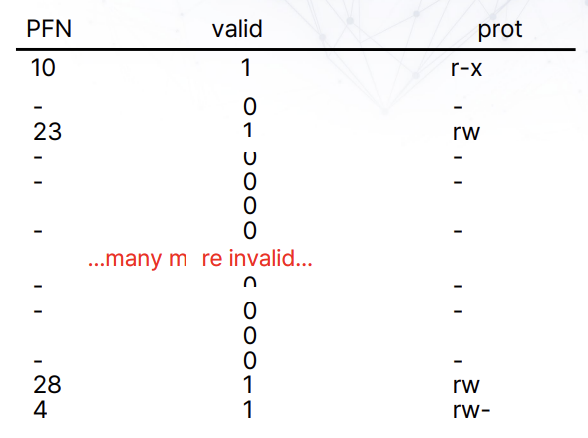
PTE를 잘 보면, 보통 연속적으로 valid한 경우가 많다. 이 부분을 segmentation으로 나눠서 관리하는 방식이다. 일반적으로 code, heap, stack으로 구분해서 사용한다. 사용하는 주소체계는 다음과 같다.

각 segmentation에 해당하는 page table이 있고, page number를 통해 PTE를 찾아 PA를 완성한다.
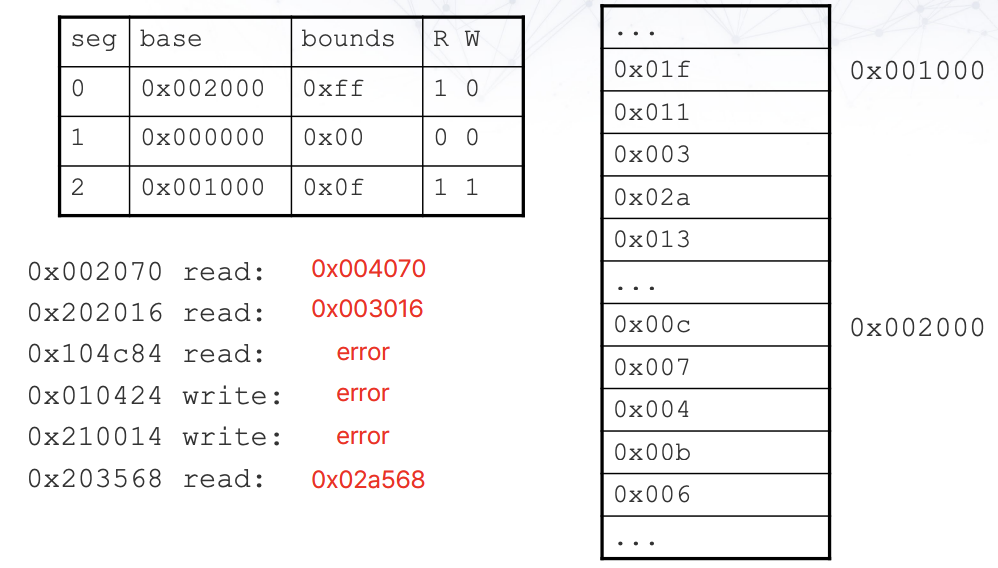
- 0x002070
4 bits -> 0x0 -> seg0 -> base = 0x002000, limit 0xff
8 bits -> 0x02 -> 0x002002 -> 0x004
12 bits -> 0x070
PA = 0x004070
| Advantages | Disadvantages |
| Segment - PT 크기 감소 - 안쓰면, 안만듦 Page - External fragmentation 없음 - Swap하면서 프로세스 동작 가능 공통 - Sharing이 더 용이해짐 |
- 매우 큰 page table이 사용될 수 있음 * 2 bits for segment * 18 bits for page * 12 bits for offset * PTE = 4 bytes PT = 2^18 * 4 bytes = 1MB Whole = 2^2 * 1MB = 4MB |
Multi-level page table
Contiguous하게 사용되는 page를 잘게 쪼개서 non-contiguously 만드는 것이 목표이다. 이를 위해 여러 level로 page table을 구성하게 된다. 주소 체계는 다음과 같다.
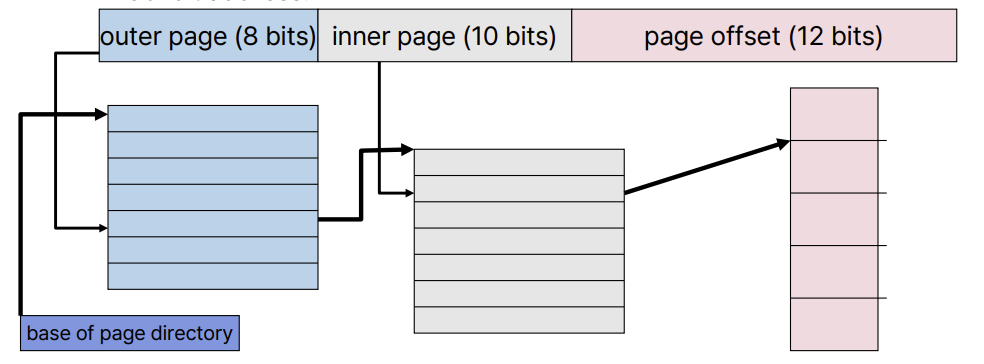
Outer page table을 page directory라고 부르며, 사용되는 page만 할당해서 구현하게 된다. Outer와 inner의 bit는 page size에 의해서 결정된다.
- Page size: 4KB
- PTE size: 4MB (assume)
- Page size = PTE size * # of PTE
2^12 = 2^2 * # of PTE
# of PTE = 2^10 - Inner page bit = 10
- So, outer page bit = 30 - 10 - 12 = 8
30 bits였으니 8 bits만으로 page directory를 구현할 수 있었다. 만약 64 bits라면 어떻게 해야 할까? 계산대로라면 42 bits를 PD 구현에 사용해야 한다. 그러면 PD가 page에 표현할 수 없기 때문에, PD의 PD를 구현하는 식으로 multi-level을 만들면 된다. 이때 level당 page table의 크기는 다음과 같이 구할 수 있다.
- 아까랑 상황은 같다.
- 4KB / 4B = 1K, level당 1K entries를 표현해야 함을 의미한다.
- level 1: 1K * 4K = 4MB
- level 2: 1K * 1K * 4K = 4GB
- level 3: 1K * 1K * 1K * 4K = 4TB
이 시스템을 TLB와 함께 사용한다고 생각했을 때, miss cost를 고려해봐야 한다. Level이 늘어날수록, lookup에 대한 비용이 커지기 때문이다. 계산해보면 다음과 같다.

다음의 명령어들에 대한 physical accesses를 계산해본다.
(A) 0xAA10: movl 0x1111, %edi
0xAA: (TLB miss=3 addr trans) + 1 instr fetch
0x11: (TLB miss=3 addr trans) + 1 movl into %edi
총 8번
(B) 0xBB13: addl &0x3, %edi
0xBB: (TLB hit) 1 instr fetch from 0x9113
총 1번
(C) 0x0519: movl %edi, 0xFF10
0x05: (TLB miss=3 addr trans) + 1 instr fetch
0xFF: (TLB hit) + 1 movl into 0x2310
총 5번
'Study > Operating System' 카테고리의 다른 글
| 6. Threads (1) | 2023.12.08 |
|---|---|
| 5. Virtual Memory (0) | 2023.12.08 |
| 3. Memory Virtualization (0) | 2023.12.01 |
| 2. CPU Virtualization (1) | 2023.11.27 |
| 1. Introduction (0) | 2023.11.21 |
